

Let \(D\) be a nonempty subset of \(\mathbb
Any constant function \(f: D \rightarrow \mathbb
If \(f: D \rightarrow \mathbb
Let \(f: \mathbb
Let \(f:[-3,2] \rightarrow \mathbb
Let \(D\) be a nonempty subset of \(\mathbb
If a function \(f: D \rightarrow \mathbb
Solution
which shows \(f\) is Lipschitz with \(\ell=1 /(2 \sqrt)\).
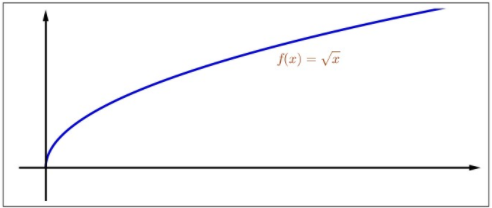
Figure \(3.4\): The square root function.
Indeed, suppose by contradiction that \(f\) is Lipschitz continuous on \(D\). Then there exists a constant \(\ell>0\) such htat
Thus, for every \(n \in \mathbb\), we have
\[\sqrt \leq \ell \text < or >n \leq \ell^ \text < for every >n \in \mathbb .\]
This is a contradiction. Therefore, \(f\) is not Lipschitz continuous on \(D\).
Let us show that \(f\) is Hölder continuous on \(D\). We are going to prove that
The inequality in (3.9) holds obviously for \(u = v = 0\). For \(u > 0\) or \(v > 0\), we have
Note that one can justify that inequality
by squaring both sides since they are both positive. Thus, (3.9) is satisfied.
While every uniformly continuous function on a set \(D\) is also continuous at each point of \(D\), the converse is not true in general. The following example illustrates this point.
Let \(f:(0,1) \rightarrow \mathbb\) be given by
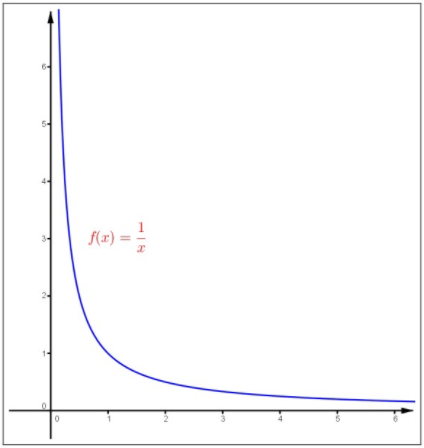
Figure \(3.5\): Continuous but not uniformly continuous on \((0, \infty)\).
Solution
We already know that this function is continuous at every \(\bar \in(0,1)\). We will show that \(f\) is not uniformly continuous on \((0,1)\). Let \(\varepsilon = 2\) and \(\delta > 0\). Set \(\delta_=\min \\), \(x=\delta_\), and \(y=2 \delta_\). Then \(x,y \in (0,1)\) and \(|x-y|=\delta_
This shows \(f\) is not uniformly continuous on \((0,1)\).
The following theorem offers a sequential characterization of uniform continuity analogous to that in Theorem 3.3.3.
Let \(D\) be a nonempty subset of \(\mathbb\) and \(f: D \rightarrow \mathbb\). Then \(f\) is uniformly continuous on \(D\) if and only if the following condition holds
(C) for every two sequences \(\left\\right\>\), \(\left\\right\>\) in \(D\) such that \(\lim _\left(u_-v_\right)=0\), it follows that \(\lim _\left(f\left(u_\right)-f\left(v_\right)\right)=0\).
Proof
To prove the converse, assume condition (C) holds and suppose, by way of contradiction, that \(f\) is not uniformly continuous. Then there exists \(\varepsilon_>0\) such that for any \(\delta > 0\), there exists \(u,v \in D\) with
Thus, for every \(n \in \mathbb\), there exist \(u_, v_ \in D\) with
\[\left|u_-v_\right| \leq 1 / n \text < and >\left|f\left(u_\right)-f\left(v_\right)\right| \geq \varepsilon_ .\]
It follows that for such sequences, \(\lim _\left(u_-v_\right)=0\), but \(\left\
Using this theorem, we can give an easier proof that the function in Example 3.5.6 is not uniformly continuous.
Solution
Consider the two sequences \(u_=1 /(n+1)\) and \(v_=1 / n\) for all \(n \geq 2\). Then clearly, \(\lim _\left(u_-v_\right)=0\), but
The following theorem shows one important case in which continuity implies uniform continuity.
Let \(f: D \rightarrow \mathbb\) be a continuous function. Suppose \(D\) is compact. Then \(f\) is uniformly continuous on \(D\).
Proof
Suppose by contradition that \(f\) is not uniformly continuous on \(D\). Then there exists \(\varepsilon_>0\) such that for any \(\delta > 0\), there exists \(u,v \in D\) with
Thus, for every \(n \in \mathbb\), there exists \(u_, v_ \in D\) with
\[\left|u_-v_\right| \leq 1 / n \text < and >\left|f\left(u_\right)-f\left(v_\right)\right| \geq \varepsilon_ .\]
Since \(D\) is compact, there exist \(u_ \in D\) and a subsequence \(\left\>\right\>\) of \(\left\\right\>\) such that
\[u_> \rightarrow u_ \text < as >k \rightarrow \infty .\]
for all \(k\) and, hence, we also have
\[v_> \rightarrow u_ \text < as >k \rightarrow \infty .\]
By the continuity of \(f\),
\[f\left(u_>\right) \rightarrow f\left(u_\right) \text < and >f\left(v_>\right) \rightarrow f\left(u_\right) .\]
Therefore, \(f\) converges to zero, which is a contradiction. The proof is now complete.
We now prove a result that characterizes uniform continuity on open bounded intervals. We first make the observation that if \(f: D \rightarrow \mathbb\) is uniformly continuous on \(D\) and \(A \subset D\), then \(f\) is uniformly continuous on \(A\). More precisely, the restriction \(f_<\mid A>: A \rightarrow \mathbb\) is uniformly continuous on \(A\) (see Section 1.2 for the notation). This follows by noting that if \(|f(u)-f(v)|
Let \(a,b \in \mathbb\) and \(a < b\). A function \(f:(a, b) \rightarrow \mathbb\) is uniformly continuous if and only if \(f\) can be extended to a continuous function \(\tilde:[a, b] \rightarrow \mathbb\) (that is, there is a continuous function \(\tilde:[a, b] \rightarrow \mathbb\) such that \(f=\tilde_<\mid(a, b)>\)).
Proof
Suppose first that there exists a continuous function \(\tilde:[a, b] \rightarrow \mathbb\) such that \(f=\tilde_<\mid(a, b)>\). By Theorem 3.5.4, the function \(\tilde\) is uniformly continuous on \([a,b]\). Therefore, it follows from our early observation that \(f\) is uniformly continuous on \((a,b)\).
For the converse, suppose \(f:(a, b) \rightarrow \mathbb\) is uniformly continuous. We will show first that \(\lim _> f(x)\) exists. Note that the one sided limit corresponds to the limit in Theorem 3.2.2. We will check that the \(\varepsilon-\delta\) condition of Theorem 3.2.2 holds.
By its definition \(\tilde_<\mid(a, b)>=f\) and, so, \(tilde\) is continuous at every \(x \in (a,b)\). Moreover, \(\lim _> \tilde(x)= \lim _> f(x)=\tilde(a)\) and \(\lim _> \tilde(x)=\lim _> f(x)=\tilde(b)\), so \(\tilde\) is also continuous at \(a\) and \(b\) by Theorem 3.3.2. Thus \(\tilde\) is the desired continuous extension of \(f\). \(\square\)
Prove that each of the following functions is uniformly continuous on the given domain:
Add texts here. Do not delete this text first.
Prove that each of the following functions is not uniformly continuous on the given domain:
Add texts here. Do not delete this text first.
Determine which of the following functions are uniformly continuous on the given domains.
Add texts here. Do not delete this text first.
Let \(D \subset \mathbb\) and \(k \in \mathbb\). Prove that if \(f, g: D \rightarrow \mathbb\) are uniformly continuous on \(D\), then \(f+g\) and \(kf\) are uniformly continuous on \(D\).
Answer
Add texts here. Do not delete this text first.
Give an example of a subset \(D\) of \(\mathbb\) and uniformly continuous functions \(f, g: D \rightarrow \mathbb\) such that \(fg\) is not uniformly continuous on \(D\).
Answer
Add texts here. Do not delete this text first.
Let \(D\) be a nonempty subset of \(\mathbb\) and let \(f: D \rightarrow \mathbb\). Suppose that \(f\) is uniformly continuous on \(D\). Prove that if \(\left\\right\>\) is a cauchy sequence with \(x_ \in D\) for every \(n \in \mathbb\), then \(\left\
Answer
Add texts here. Do not delete this text first.
Let \(a,b \in \mathbb\) and let \(f:(a, b) \rightarrow \mathbb\).
Add texts here. Do not delete this text first.
Let \(f\) be a continuous function on \([a, \infty)\). Suppose
Answer
Add texts here. Do not delete this text first.